PRODUCTO VECTORIAL DE DOS VECTORES
Es ahora, al referirnos al producto vectorial, cuando al signo de multiplicar lo representamos con el aspa o cruz de ahí que también llamemos producto cruz.
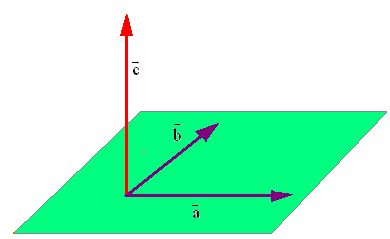
El producto vectorial de dos vectores produce un vector 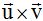 perpendicular a los dos vectores.
perpendicular a los dos vectores.
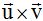 perpendicular a los dos vectores.
perpendicular a los dos vectores.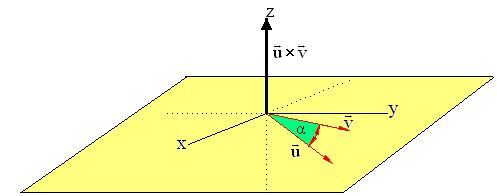
En la siguiente figura, el producto vectorial de los dos vectores situados en el plano: 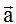 y
y 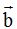 es un nuevo vector
es un nuevo vector 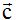 .
.
Este vector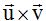 o
o  tienes las siguientes características:
tienes las siguientes características:
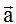 y
y 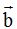 es un nuevo vector
es un nuevo vector 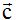 .
.
Este vector
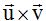 o
o 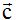 tienes las siguientes características:
tienes las siguientes características:
Características del vector 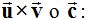
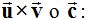
Todo vector tiene sus propias particularidades como son: sumódulo, su dirección y su sentido.
Vamos a estudiar el valor del módulo del vector 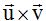 , su dirección y sentido.
, su dirección y sentido.
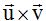 , su dirección y sentido.
, su dirección y sentido.
Módulo:
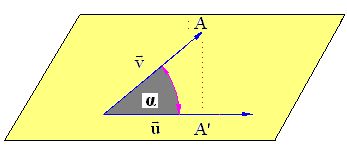
En la figura siguiente tenemos un plano donde hemos dibujado los vectores 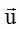 y
y 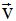 :
:
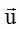 y
y 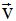 :
: 
El 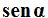 será igual al cateto opuesto al ángulo dividido por la hipotenusa:
será igual al cateto opuesto al ángulo dividido por la hipotenusa:
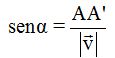
 será igual al cateto opuesto al ángulo dividido por la hipotenusa:
será igual al cateto opuesto al ángulo dividido por la hipotenusa: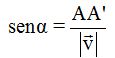
Podemos escribir también:
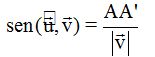
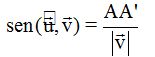
de donde vemos que : 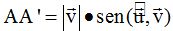
Si multiplicamos a los dos miembros de la igualdad por el módulo de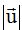 tenemos:
tenemos:
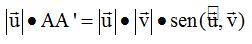
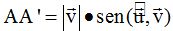
Si multiplicamos a los dos miembros de la igualdad por el módulo de
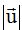 tenemos:
tenemos: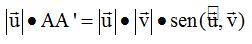
El producto 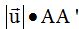
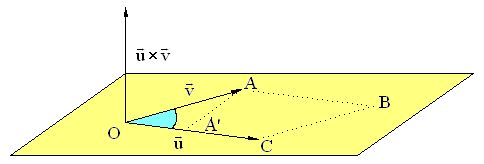
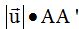
equivale a la superficie del paralelogramo OABC:

La base es 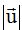 y la altura
y la altura 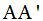
También podemos expresar la superficie del paralelogramo OABC con el producto:
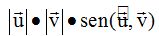
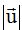 y la altura
y la altura 
También podemos expresar la superficie del paralelogramo OABC con el producto:
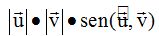
Como hemos dicho que a 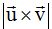 equivale a:
equivale a:
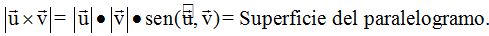








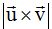 equivale a:
equivale a: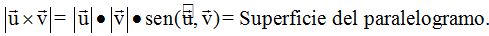
Según vemos en la línea anterior, el módulo del producto vectorial equivale al área del paralelogramo que está definido por los dos vectores.
Ángulo que forman dos vectores
1 Enunciado
Calcula el angulo que forman los vectores  y
y  . Calcula también los cosenos directores de ambos vectores.
. Calcula también los cosenos directores de ambos vectores.
 y
y  . Calcula también los cosenos directores de ambos vectores.
. Calcula también los cosenos directores de ambos vectores.2 Solución
El producto escalar de dos vectores es

siendo θ el ángulo que forman los vectores. Es decir

Como están expresados en una base cartesiana es fácil hacer estas operaciones. El producto escalar es

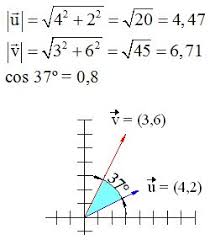
Los módulos de los vectores son

El coseno del ángulo es

El ángulo es

Los cosenos directores son los cosenos de los ángulos que forma el vector con los ejes coordenados. Para el vector  tenemos
tenemos
 tenemos
tenemos
Puede comprobarse que cos2αx + cos2αy + cos2αz = 1.00
Para el vector  tenemos
tenemos
 tenemos
tenemos
EJEMPLO:
No hay comentarios:
Publicar un comentario